알고리즘은 시간복잡도 빅오를 상수,로그,선형,선형로그,이차시간,지수시간,팩토리얼보고 공간복잡도를 메모리양으로 생각한다.
시간과 공간 효율성은 자료구조를 알고나서 좀더 생각해보자.
자료구조는 배열,연결리스트,스택,큐,힙(PriorityQueue- 완전이진트리),트리,그래프,해시 등이 있다.
배열과 리스트는.. [] 와 index로 넘어가고
스택은 LIFO로 호출에 좋고, 큐는 FIFO로 순서적인 계산대를 생각하면 되었고,
힙은 최댓값, 최솟값을 구하는데 좋다. 마지막을 제외한 모든 노드에서 자식들이 꽉 채워진 이진트리이다.(중복허용)
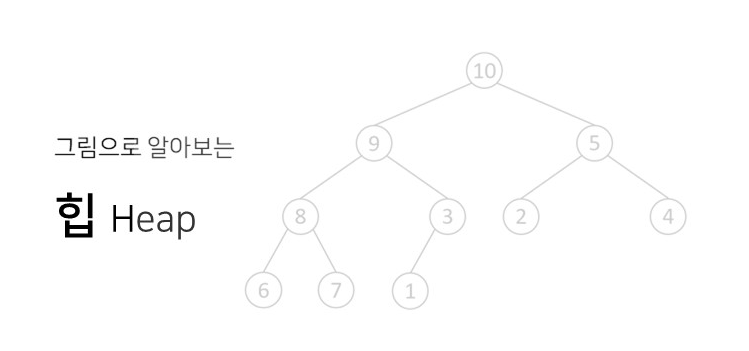
트리와 그래프는 비선형 자료구조이며 노드와 간선으로 구성된다. 그리고 둘다 특정순회방법(DFS, BFS) 등을 사용하여 노드를 방문할 수 있다. 차이점이라면 트리는 계층구조(root노드 존재,cycle x)고 그래프는 네트워크구조(모든 노드 동등, cycle o)이다.

위의 그래프를 코드로 표현해보면 다음과 같다.
import java.util.ArrayList;
import java.util.List;
class Graph {
private int numVertices;
private List<List<Integer>> adjList;
// 그래프 초기화
public Graph(int numVertices) {
this.numVertices = numVertices;
adjList = new ArrayList<>(numVertices);
for (int i = 0; i < numVertices; i++) {
adjList.add(new ArrayList<>());
}
}
// 간선 추가
public void addEdge(int src, int dest) {
adjList.get(src).add(dest);
adjList.get(dest).add(src); // 무방향 그래프이므로 양쪽에 간선을 추가
}
// 그래프 출력
public void printGraph() {
for (int i = 0; i < numVertices; i++) {
System.out.print("Vertex " + i + ":");
for (Integer vertex : adjList.get(i)) {
System.out.print(" -> " + vertex);
}
System.out.println();
}
}
public static void main(String args) {
// 정점의 개수는 4개 (A, B, C, D)
Graph graph = new Graph(4);
// 정점 A, B, C, D를 각각 0, 1, 2, 3으로 매핑
graph.addEdge(0, 1); // A - B
graph.addEdge(0, 2); // A - C
graph.addEdge(1, 2); // B - C
graph.addEdge(1, 3); // B - D
graph.addEdge(2, 3); // C - D
// 그래프 출력
graph.printGraph();
}
}
해시는 키/값을 저장하는 해시함수를 사용해서 빠르게 검색한다. 뭐 map타입으로 hashmap을 잘 사용한다.
알고리즘은 그리드(힙,큐)와 탐색알고리즘(트리)이 중요하다. 그러나 기초는 입력과 출력을 여러개를 하나로 하나를 여러개로 하는것부과 문자열조작부터 시작해야 한다고 하니..
d (깊이) fs 알고리즘은 호출이 편한 재귀나 스택 자료구조를 쓰고, b(넓이)fs 알고리즘은 우선순위가 가능한 큐 자료구조를 주로 쓴다.
그리드알고리즘은 최댓값 최솟값의 우선순위가 중요한 힙이나 순서가 중요한 큐를 쓸것이고,
탐색알고리즘은 계층적으로 구조화된 트리 자료구조 쓴다고 보자~!
class TreeNode {
char value;
TreeNode left;
TreeNode right;
// 노드 생성자
public TreeNode(char value) {
this.value = value;
this.left =;
this.right =;
}
}
class BinaryTree {
TreeNode root;
// 트리 생성자
public BinaryTree(char rootValue) {
root = new TreeNode(rootValue);
}
// 전위 순회 (Preorder Traversal)
public void preOrderTraversal(TreeNode node) {
if (node !=) {
System.out.print(node.value + " ");
preOrderTraversal(node.left);
preOrderTraversal(node.right);
}
}
// 중위 순회 (Inorder Traversal)
public void inOrderTraversal(TreeNode node) {
if (node !=) {
inOrderTraversal(node.left);
System.out.print(node.value + " ");
inOrderTraversal(node.right);
}
}
// 후위 순회 (Postorder Traversal)
public void postOrderTraversal(TreeNode node) {
if (node !=) {
postOrderTraversal(node.left);
postOrderTraversal(node.right);
System.out.print(node.value + " ");
}
}
public static void main(String args) {
// 트리 생성
BinaryTree tree = new BinaryTree('A');
tree.root.left = new TreeNode('B');
tree.root.right = new TreeNode('C');
tree.root.left.left = new TreeNode('D');
tree.root.left.right = new TreeNode('E');
tree.root.right.right = new TreeNode('F');
// 트리 순회 출력
System.out.print("전위 순회: ");
tree.preOrderTraversal(tree.root);
System.out.println();
System.out.print("중위 순회: ");
tree.inOrderTraversal(tree.root);
System.out.println();
System.out.print("후위 순회: ");
tree.postOrderTraversal(tree.root);
System.out.println();
}
}
'4차산업혁명의 일꾼 > Java&Spring웹개발과 서버 컴퓨터' 카테고리의 다른 글
| 코테, 포폴에 밀리는 OCJP(OCAJP, OCPJP)와 프로그래머스 아이패드 이벤트 (0) | 2024.08.01 |
|---|---|
| 스프링시큐리티6(OAuth2)의 속도, 자원절감, 보안향상, 권한조정의 이점 (0) | 2024.07.21 |
| 클라우드시대에 2025년부터 지원 끊기는 이유 WebFlux(Spring5), 클라우드 시대에 절약과 함께 빛나는 AOT엔진의 Spring6 ~! (0) | 2024.07.18 |
| 자바의 희망 구독/서브모델의 Kafka , 대용량처리 관련 캐쉬하는 Redis, 장애예방 CircuitBreaker, 장애대응책 RetryConfig (0) | 2024.07.18 |
| 스프링 기본개념과 변천사 그리고 스프링버전5이상 혹은 스프링부트3의 필요성에 관하여 (2) | 2024.07.13 |