※ 수학의 정의
수학은 토지측량, 천문관찰의 도구로 활용되고, 그리스(BC400) 에서 유클리드 기하학이 유명해서 신전에 기하학을 모르면 들어오지 말라고 할정도 였다. 그 뒤 17C 뉴턴,라이프니츠에의해 미적분학이 발전 했다.
18C 수학자 스위스의 오일러는 논문 500편을 썼다.
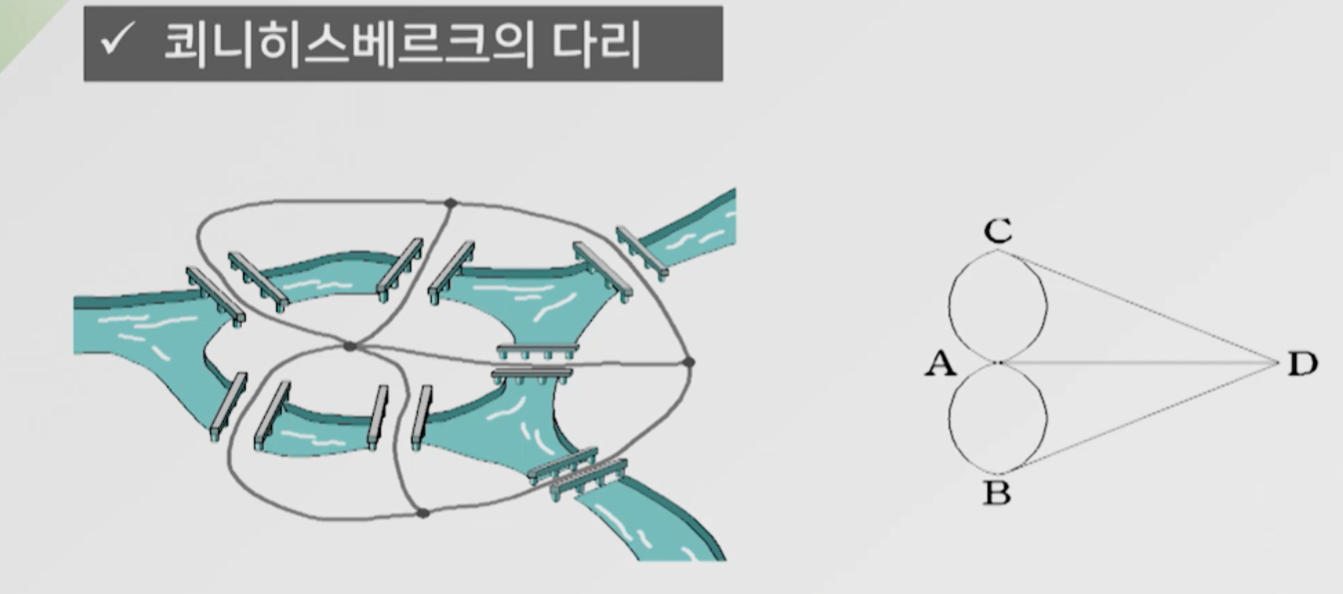
오일러가 한붓그리기로 추상화해서 다리 한번만 건너면서 모두 건너는 것이 불가능함을 증명했다.

홀수점의 개수가 0,2개 여야만 한다고 했다.
다리건너기 문제를 한붓그리기로 추상화하고 , 그 다음에 홀수점의 갯수가 0,2개 여야만 한붓그리기가 가능함을 증명했다.
이것은 그래프와 네트워크에 응용되었다.

지구 둘레를 구하기 위해, 지구의 중심부의 7.2도를 추상화시켜 925km 정도 된다는 것을 문제화한 후,
이를 수학적 원리로 해결했다.

지구둘레 = 46,520 km 를 구한 것이다.
※ 수학의 기초논리
명제의 증명 3가지 방법은 연역법(몇개의 명제가 옳으므로 다른 명제가 옳다는 것을 논리적으로 증명), 귀류법(명제의 결론을 부정하여 그 결론이 성립하지 않으면 모순이 발생) ,귀납법(자연수에 대한 명제가 모든 자연수에 대해 성립함을 보이는 증명방법)
※ 수의 체계와 성질
실수는 유리수와 무리수로 구분되고,
유리수는 정수와 정수가 아닌 유리수로 구분되며,
정수는 자연수와 0, 음수로 구분된다.

실수는 유리수와 무리수를 합해 실직선위에 보일수 있기에 대소 비교가 가능하다.

실수는 실직선상에 있어서,
대소비교가 가능하기 때문에
교환법칙, 결합법칙, 분배법칙, 항등원,역원이 성립한다.

위의 내용을 정리하면,
- 수학은 현실 문제를 추상화 또는 일반화하여 그 문제를 논리적으로 해결할 수 있는 학문이다.
- 수학의 명제는 연역법, 귀류법, 수학적 귀납법으로 증명한다.
- 실수는 유리수와 무리수로 구성되어 있다. 두 실수가 있다면 대소의 순서가 있고 덧셈과 곱셈에 대해 교환법칙, 결합법칙, 분배법칙이 성립하며 항등원과 역원이 존재한다.
- 두 실수 사이의 모든 점의 모임을 구간이라고 한다.
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
수학에 대해서 보니까
수학은 실제로 자연세계를 이해하려 할때
추상화된 기호를 가지고,
상황을 문제화하여,
결과를 도출해 내는 것이다.
결과를 도출해내는데 있어서 논리가 동원되는데
원인으로 인한 연역법, 결과로 인한 귀납법, 결과부정으로 위한 귀류법 등의 논리로 증명한다.
실수(유리수,무리수)의 체계를 가지고
수의 성질을 보면 덧셈,곱셈으로 교환법칙, 분배법칙, 결합법칙등의 논리적 성질을 가진다.
항등원이나 역원은 수의 방향을 생각하기 위한 성질 같다.
'4차산업혁명의 일꾼 > 웹개발' 카테고리의 다른 글
| Redhat 무료판 CentOS의 대안 Rocky Linux를 VMware(가상환경)에 띄워보자 (0) | 2023.08.17 |
|---|---|
| 골동품이 생각나는 멀티미디어와 진행되어야할 프로젝트 (0) | 2023.08.16 |
| 오픈소스 진영의 리눅스 소개 미국의 대학들(버클리,MIT,하버드)에 대한 끄적임 (0) | 2023.08.16 |
| 클라우드컴퓨팅의 기본 이해와 네트워크 속도 고찰 (0) | 2023.08.16 |
| 우아한테크코스 Lock & JPA Lock (0) | 2023.08.14 |